 |
Love.az |
Bu məqalədəki məlumatların yoxlanıla bilməsi üçün əlavə mənbələrə ehtiyac var. Lütfən, məqaləyə etibarlı mənbələr əlavə edərək onu təkmilləşdirməyə kömək edin. Mənbəsiz məzmun problemlər yarada və silinə bilər. Problemlər həll edilməmiş şablonu məqalədən çıxarmayın. Daha ətraflı məlumat və ya məqalədəki problemlərlə bağlı müzakirə aparmaq üçün məqalənin müzakirə səhifəsinə diqqət yetirə bilərsiniz. |
Bu məqaləni vikiləşdirmək lazımdır. Lütfən, məqaləni ümumvikipediya və redaktə qaydalarına uyğun şəkildə tərtib edin. |
Radian (ixtisarı: rad; lat. radius — şüa, radius) — müasir riyaziyyatda və fizikada müstəvi bucaqların əsas ölçü vahidi. Radian, qövsün bucaq ölçüsü ilə təyin edilir.
| Radian | |
|---|---|
 | |
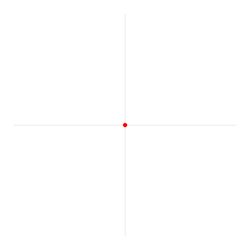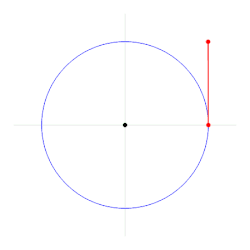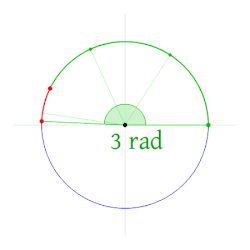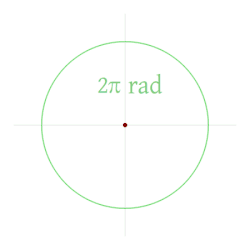

Belə olduqda, tam çevrənin radianla ölçüsü 2π radiana bərabərdir.
Başqa bucaq ölçüləri ilə müqayisə:
Dərəcə/radian çevrilmələri
Radianı dərəcəyə çevirmək üçün göstərilən radianı nisbətinə vurmaq lazımdır:
Dərəcəni radiana çevirmək üçün göstərilən dərəcəni nisbətinə vurmaq lazımdır.
Riyazi analizdə, triqonometrik funksiyalara baxılarkən, arqument həmişə radianla ifadə edilir.
Kiçik bucaqlar olduqda sinus və radianla ifadə edilmiş bucağın tangensi təxminən bu bucağın özünə bərabərdir ki, bu da yuvarlaq hesablamalar zamanı istifadə olunur: