 |
Love.az |
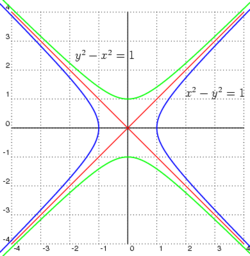
Hiperbola (yun. ύπερβολή — yuxarıdan, ύπερ — atmaq) — tərs mütənasibliyin qrafikinə verilən addır.
Tərs mütənasiblik düsturu
y = k ÷ x
Hiperbolanın asimptotları:
Hiperbola 2 asimptotdan ibarətdir:
Hiperbola Parabolanın tərsidir. Hiperbola iki budaqdan ibarətdir. k > 0 olduqda hiperbolanın budaqları I və III rüblərdə, k < 0 olduqda isə hiperbolanın budaqları II və IV rüblərdə yerləşir. Hiperbolanın xarakteristikasına aşğıdakı ifadələr aiddir:
| Vikianbarda Hiperbola ilə əlaqəli mediafayllar var. |